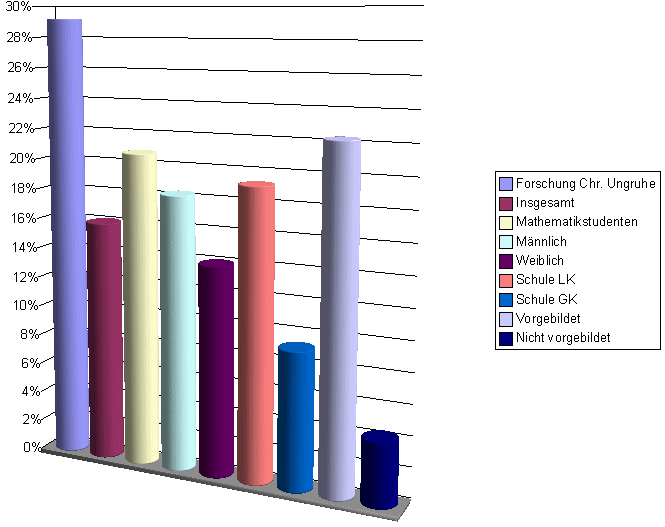Inhaltsverzeichnis
Didaktik der Wahrscheinlichkeit
Ausarbeitung im Rahmen des Proseminars Didaktik der Mathematik „Didaktik der Elementaren Stochastik“ im SS 2001 an der Universität Osnabrück unter Dr. Johann Sjuts.
Ausarbeitung
Da die Ausarbeitung mathematische Symbole enthält, die (noch) nicht in HTML integriert sind, gibt es die Ausarbeitung nur als .PDF-Datei.
Forschung
Zielgruppe
Das Ziel der Forschung war es, festzustellen, wie gut Studenten, die am Anfang ihres Studiums stehen und entweder Mathematik studieren oder dieses im Rahmen ihres Studiums belegen müssen, Aufgaben, die die Wahrscheinlichkeit betreffen, lösen können. Um dieses Ziel zu erfüllen habe ich den Studenten der Veranstaltung „Analysis I“, die auch in diesem Semester an der Universität Osnabrück unter Prof. Meyer-Nieberg angeboten wird, einen anonymen Test gestellt. Die Teilnahme war freiwillig, weswegen auch nur 71 der ca. 130 Teilnehmer dieser Veranstaltung daran teilnahmen. Die „Analysis I“-Veranstaltung hat nichts mit Wahrscheinlichkeit zu tun, von daher möge bitte keiner auf die Idee kommen, die Ergebnisse - seien sie jetzt positiv oder negativ - auf die Veranstaltung von Prof. Meyer-Nieberg zurückzuführen. Ich möchte Prof. Meyer-Nieberg und seinem Assistenten Christian Möller jedoch ganz herzlich danken, dass sie sich bereit erklärt haben, mich bei diesem Test zu unterstützen, und mir dazu sogar 15 Minuten der Vorlesungszeit geschenkt haben.
Test
Die Aufgaben des Tests sind nicht willkürlich sondern bewußt gewählt, um zusätzlich Vergleichsmöglichkeiten zu haben. Die erste Aufgabe habe ich von Christoph Ungruhe, der in seiner Forschung, die er in der Sitzung vor mir vorgestellt hatte, Schüler verschiedener Gymnasien getestet hatte. Die letzten drei Aufgaben sind den Beispielaufgaben der Population 3 der TIMSS-Studie (TIMSS/III - Abschlußklassen der Sekundarstufe II an allgemeinbildenden und beruflichen Schulen) entnommen, die für einigen Wirbel gesorgt hat. Im Einzelnen sind das: Aufgabe 2) L10, Aufgabe 3) L14 und Aufgabe 4) K11 in der jeweils offiziellen deutschen Übersetzung. Zu den Aufgaben kamen noch einige statistische Informationen, die ich zur späteren Auswertung verwendet habe. Die Studenten hatten 20 Minuten Zeit, um den Test zu lösen.
Im folgenden können Sie sich den Test so runterladen bzw. anschauen, wie er den Studenten vorgelegt wurde.
Dass die Aufgaben alle vom Typ multiple choice sind, hat mehrere Gründe, der Hauptgrund ist wohl, dass sie leicht statistisch auszuwerten sind. Man muß natürlich im Hinterkopf behalten, dass „intelligentes Raten“ auch zu Lösungen führen kann, die als richtig bewertet werden, auch wenn die Gedanken des Studenten vollkommen falsch gewesen sein mögen. Aus Gründen der Vergleichbarkeit bin ich jedoch dabei geblieben und habe die Aufgaben wort-wörtlich übernommen.
Lösungen der Aufgaben
Aufgabe 1
Die Lösung ist, dass es egal ist. Für diese Aufgabe gibt es zwei verschiedene Lösungswege, die unterschiedlich schwierig sind.
Lösungsweg 1
Wenn zwei Personen aus einer Urne mit 50 Kugeln jeweils abwechselnd eine Kugel ziehen, so endet jede Person mit 25 Kugeln. Ist nun eine der Kugeln weiß und die anderen schwarz, so ist die Wahrscheinlichkeit, dass die Kugel bei einer bestimmten Person ist, genau 1/2. Somit ist es egal, ob als erster oder als zweiter gezogen wird.
Lösungsweg 2
Man kann sich den Vorgang als Baum bedingter Wahrscheinlichkeiten vorstellen. In dem Fall ist die Wahrscheinlichkeit, dass die erste Person die weiße Kugel zieht 1/50 + 49/50 ⋅ 48/49 ⋅ 1/48 + 49/50 ⋅ 48/49 ⋅ 47/48 ⋅ 46/47 ⋅ 1/46 + … + 49/50 ⋅ 48/49 ⋅ 47/48 ⋅ … ⋅ 2/3 ⋅ 1/2 = 1/2. Da die Summe der Wahrscheinlichkeiten 1 ist, ist es demnach egal, ob man zuerst oder als zweiter zieht.
Lösungsweg 3
Behauptung: Wenn in einer Urne eine gerade Anzahl (2⋅n) Kugeln liegen und genau eine davon andersfarbig ist und zwei Personen abwechselnd aus dieser Urne ziehen, so ist die Wahrscheinlichkeit, dass eine bestimmte Person die andersfarbige Kugel zieht, 1/2.
Beweis (durch Induktion nach n):
n=1: Bei zwei Kugeln ist die Wahrscheinlichkeit, dass die Person, die als erste zieht, die andersfarbige Kugel zieht, 1/2. Demnach ist für die andere Person die Wahrscheinlichkeit auch 1/2.
n → n+1: Wenn aus einer Urne mit 2⋅(n+1) = 2⋅n+2 Kugeln zwei Kugeln gezogen sind und die andersfarbige Kugel noch in der Urne ist, so ist dies eine Urne mit 2 ⋅ n Kugeln, für die per Induktionsvoraussetzung die Wahrscheinlichkeit 1/2 für beide Personen ist, die andersfarbige Kugel zu ziehen. Es gibt noch zwei weitere Fälle: Die Kugel wird im ersten Zug von der einen oder im zweiten Zug von der anderen Person gezogen. Im ersten Fall ist die Wahrscheinlichkeit 1/(2⋅n+2)) und im zweiten Fall (2⋅n+1)/(2⋅n+2)) ⋅ 1/(2⋅n+1) = 1/(2⋅n+2)). Somit ist die Gesamtwahrscheinlichkeit, dass die erste Person die andersfarbige Kugel zieht 1/(2⋅n+2)) + (2⋅n+1)/(2⋅n+2) ⋅ (2⋅n)/(2⋅n+1) ⋅ 1/2 = (1+n)/(2⋅n+2) = 1/2 und die Gesamtwahrscheinlichkeit, dass die zweite Person die andersfarbige Kugel zieht 1/(2⋅n+2)) + (2⋅n+1)/(2⋅n+2) ⋅ (2⋅n)/(2⋅n+1) ⋅ 1/2 = (1+n)/(2⋅n+2) = 1/2.
Da 50 eine gerade Zahl ist, gilt dieser Beweis für unsere Aufgabe.
Aufgabe 2
Die Lösung ist A. 0,995. Hier haben wir einen Fall von bedingter Wahrscheinlichkeit. Dieses zu lösen gibt es zwei verschiedene Lösungswege, die jedoch fast identisch sind.
Lösungsweg 1
Gesucht werden all die Fälle, bei denen mindestens eine Alarmanlage anspricht. Das sind die Fälle A = dass die erste anspricht, B = dass die zweite anspricht und C = dass beide ansprechen. Die Wahrscheinlichkeiten sind: P(A) = 0,95 ⋅ 0,1 = 0,095, P(B) = 0,9 ⋅ 0,05 = 0,045, P(C) = 0,95 ⋅ 0,9 = 0,855. Die Summe der Wahrscheinlichkeiten ist 0,095 + 0,045 + 0,855 = 0,995.
Lösungsweg 2
Gesucht werden all die Fälle, bei denen mindestens eine Alarmanlage anspricht. Das ist genau dann der Fall, wenn nicht keine Alarmanlage anspricht, also die Differenz zwischen dem sicheren Ereignis und dem, dass keine Anspricht. Die Wahrscheinlichkeit, dass keine anspricht ist 0,1 ⋅ 0,05 = 0,005. Demnach ist die Wahrscheinlichkeit, dass mindestens eine anspricht 1 - 0,005 = 0,995.
Aufgabe 3
Die Lösung ist 32%.
Lösungsweg
Die Anzahl derer, die rauchen und trinken, sind von 1000 Personen genau 320. Demnach ist die Wahrscheinlichkeit, dass eine der 1000 befragten Personen raucht und trinkt 320/1000 = 32/100 = 8/25 = 32%.
Aufgabe 4
Die Lösung ist D, 1/3.
Lösungsweg
Es gibt von den Zahlen 1 bis 24 genau 6 Karten, die durch 4 teilbar sind, nämlich {4, 8, 12, 16, 20, 24}. Es gibt von den Zahlen 1 bis 24 genau 4 Karten.
Auswertung
Statistische Auswertung
Als erstes steht eine statistische Auswertung der Lösungen an.
| Vergleichsdaten | |||||
|---|---|---|---|---|---|
| Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 | Anzahl der Personen | |
| TIMSS International | 29% | 51% | 50% | ||
| TIMSS Deutschland | 21% | 42% | 46% | ||
| TIMSS deutscher LK | 15% | 34% | 40% | ||
| TIMSS deutscher GK | 30% | 62% | 62% | ||
| Forschung Christoph Ungruhe | 29% | 129 | |||
| Forschung Christian Datzko | |||||
| Insgesamt | 16% | 45% | 68% | 62% | 69 |
| Mathematikstudenten | 21% | 41% | 62% | 62% | 29 |
| Männlich | 18% | 52% | 79% | 67% | 33 |
| Weiblich | 14% | 39% | 58% | 58% | 36 |
| Schule LK | 19% | 51% | 74% | 66% | 47 |
| Schule GK | 9% | 32% | 55% | 55% | 22 |
| Vorgebildet | 22% | 56% | 67% | 64% | 45 |
| Nicht vorgebildet | 4% | 25% | 71% | 58% | 24 |
In dieser Tabelle gibt die Prozentzahl die Wahrscheinlichkeit an, dass, wenn ich einen Beliebigen aus der Menge der gestesteten Personen ziehe, dieser die Aufgabe richtig gelöst. In anderen Worten ist dies die Lösungswahrscheinlichkeit der Gruppe und Aufgabe.
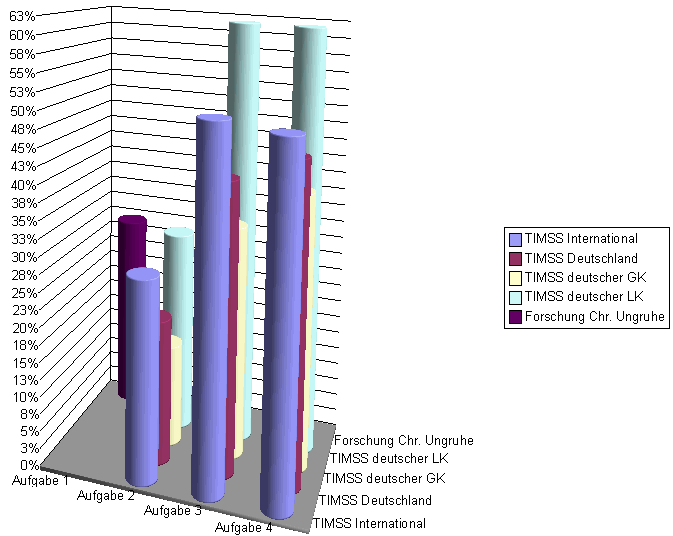
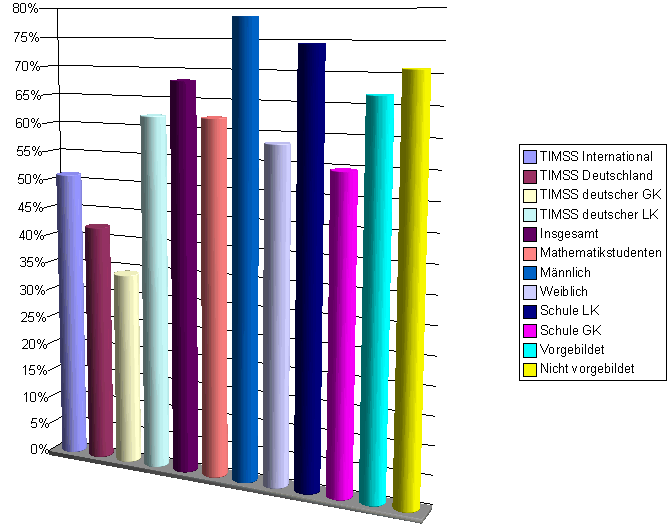
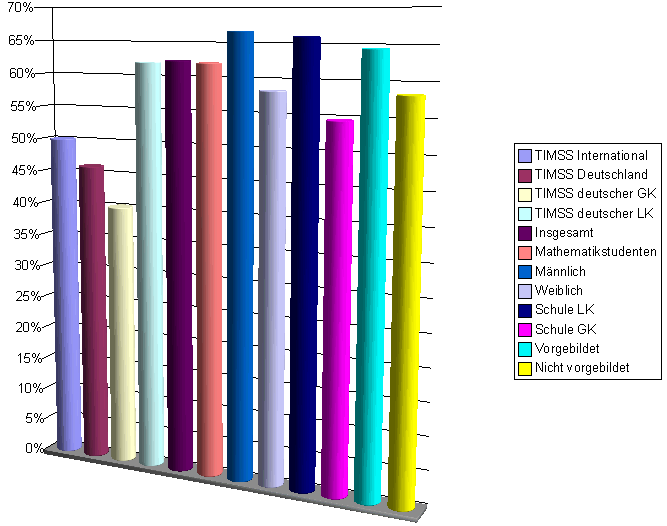
Graphisch dargestellt ist es vielleicht ein wenig anschaulicher, zuerst die Vergleichsdaten alleine und dann die Forschung insgesamt:
Vergleichsdaten
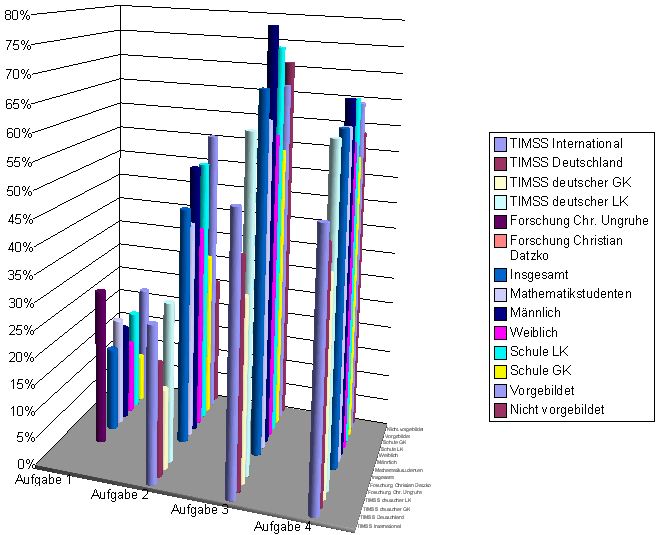
Alle Daten im Überblick
Genauere Betrachtung der Ergebnisse
Aufgabe 1
Bei der Betrachtung dieser Aufgabe fällt zuerst einmal auf, dass das Ergebnis im Vergleich zur Forschung von Christoph Ungruhe ziemlich schlecht ausgefallen ist. Festzuhalten ist folgendes: Mathematikstudenten sind besser als der Durchschnitt, männliche Studenten besser als weibliche, Studenten, die den Leistungskurs Mathematik in der Schule hatten, sind besser als die mit Grundkurs und diejenigen, die Wahrscheinlichkeit in der Schule oder im Studium hatten, sind besser als die, die es nicht hatten - hier hat sich die Ausbildung anscheinend gelohnt.
Aufgabe 1
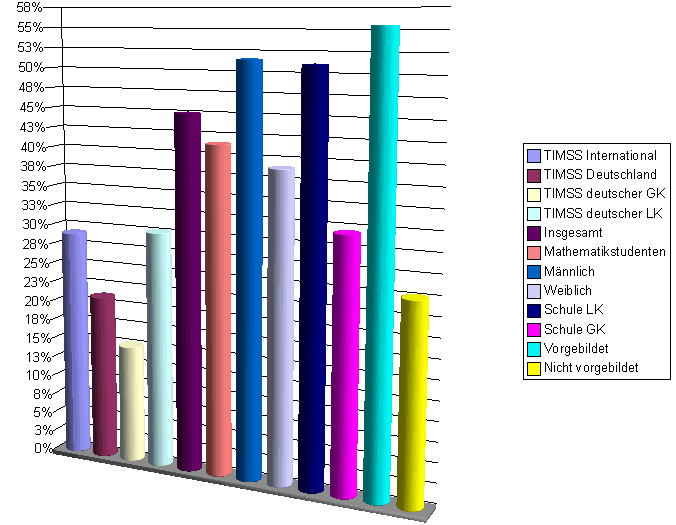
Aufgabe 2
Hier ist nun eine deutliche Verbesserung gegenüber TIMSS festzustellen. Die Mathematikstudenten sind allerdings diesmal schlechter als der Durchschnitt. Ansonsten das bekannte Bild, vielleicht etwas schärfer noch: männliche besser als weibliche, LK-Besucher besser als GK-Besucher und vorgebildete besser als nicht vorgebildete.
Aufgabe 2
Aufgabe 3
Für diese Aufgabe scheint kaum Verbesserungspotential vorhanden gewesen sein, auch sind die Unterschiede zwischen den Gruppen diesmal nicht so stark. Mathematikstudenten sind schlechter als der Durchschnitt, männlich besser als weiblich, LK besser als GK, aber die nicht vorgebildeten sind bei dieser Aufgabe besser zurande gekommen als die vorgebildeten.
Aufgabe 3
Aufgabe 4
Die letzte Aufgabe birgt auch kaum Überraschungen. Kaum besser als die TIMSS-Ergebnisse heben sich auch die Mathematikstudentenergebnisse nicht groß heraus. Ansonsten das übliche Bild: männlich besser als weiblich, LK besser als GK und vorgebildet besser als nicht vorgebildet.
Aufgabe 4
Zusammenfassung
Zusammengefasst sind die Beobachtungen folgende: Bei der Aufgabe 1 ist eine deutliche Verschlechterung der Ergebnisse festzustellen, während bei den Aufgaben 2 - 4, die mit der TIMSS/III-Studie verglichen werden, eine zumindest minimale Verbesserung festzustellen ist. Durchgehend ist es so, dass Studenten, die männlich sind, besser sind als die, die weiblich sind. Desgleichen ist festzustellen, dass Studenten, die einen Mathematik-Leistungskurs während ihrer Schulzeit besucht haben, besser sind als solche, die einen Grundkurs besucht haben. Zuletzt ist in fast allen Aufgaben (bis auf Aufgabe 3) die Vorbildung nützlich gewesen.
Exemplarische Betrachtung von Begründungen der Lösungen
Die Lösungen der Studenten und Studentinnen sind ohne Sortierschlüssel mit Nummern versehen worden, dass man bei Bedarf nachschauen könnte, was sie bei anderen Aufgaben für Lösungen gegeben haben.
Aufgabe 1
Aufgabe 1 - Lösungsversuch 1 (Studentin 3)
Diese Studentin ist leider nicht sehr weit gegangen mit ihren Überlegungen. Sie scheint sich noch nicht einmal Gedanken darüber gemacht zu haben, wie die Wahrscheinlichkeiten sind.
| Studentin 3 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alter | Geschlecht | Studienrichtung Mathe | Mathe-LK | Vorgebildet | Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 |
| 20 | W | nein | ja | ja | falsch | falsch | richtig | richtig |
Aufgabe 1 - Lösungsversuch 2 (Student 44)
Dieser Student scheint schon etwas weiter gedacht zu haben. Er hat sich Gedanken über die Wahrscheinlichkeit gemacht, dass die weiße Kugel gleich als erstes gezogen wird (1/50) und dann überlegt wie wahrscheinlich dies ist, wenn schon eine schwarze Kugel gezogen wurde (1/49). Er hat aber leider nicht konsequent zuende gedacht.
| Student 44 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alter | Geschlecht | Studienrichtung Mathe | Mathe-LK | Vorgebildet | Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 |
| 21 | M | ja | ja | ja | falsch | richtig | richtig | richtig |
Aufgabe 1 - Lösungsversuch 3 (Student 28)
Diesem Studenten muss man leider eine fehlerhafte Vorstellung von Wahrscheinlichkeit attestieren. Wenn man seine Aussage für bare Münze nähme, so wurde daraus folgern, dass die Wahrscheinlichkeit eines Ereignisses davon abhängt, dass das Ereignis schon eingetreten ist! Dabei ist es doch eher so, dass die Wahrscheinlichkeit eine Aussage darüber machen möchte, wie wahrscheinlich es ist, dass ein Ereignis eintreten wird! Es ist leider auch keine begründete Annahme möglich, dass er einen Lösungsweg gewählt hat, der adäquat ist. Dass er das richtige angekreuzt hat ist als Zufall anzusehen, dass seine verquere Vorstellung das richtige Ergebnis bringt.
| Student 52 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alter | Geschlecht | Studienrichtung Mathe | Mathe-LK | Vorgebildet | Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 |
| 23 | M | ja | ja | ja | richtig | richtig | richtig | falsch |
Aufgabe 2
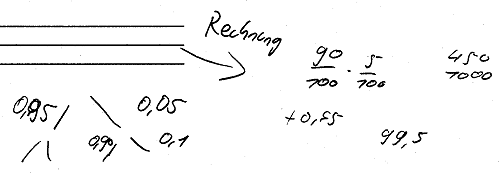
Aufgabe 2 - Lösungsversuch 1 (Student 52)
Als Begründung für die (richtige) Lösung der Aufgabe 2 hat dieser Student einfach nur diese paar Zahlen hingeschrieben, links ist eine Andeutung eines Baumes zu sehen und rechts ein paar Zahlen. Ich denke, er hat die richtige Vorstellung gehabt und auch richtig gerechnet, jedoch entweder keine Lust gehabt, es richtig zu notieren oder gar nicht die Fähigkeit dazu gehabt. Aber den Zahlen kann man entnehmen, dass seine Gedanken und Rechnungen richtig gewesen sind.
| Student 52 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alter | Geschlecht | Studienrichtung Mathe | Mathe-LK | Vorgebildet | Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 |
| 23 | M | ja | ja | ja | richtig | richtig | richtig | falsch |
Aufgabe 2 - Lösungsversuch 2 (Studentin 8)
Dieser Lösungsversuch ist ein leuchtendes Beispiel dafür, dass die Vorbildung nichts genützt hat, ich wage sogar zu behaupten, eher geschadet hat. Denn was hat sie gemacht: Sie wußte, dass man diese Aufgabe über einen Baum lösen kann, und dass man an den Ästen die Wahrscheinlichkeiten notiert. Dann werden die Ergebnisse multipliziert und addiert - aber wer wird mit wem multipliziert und wer mit wem addiert? Genau dieses hat sie dann leider vertauscht und ist konsequent zu einem Ergebnis gekommen, das vollkommen falsch ist. Per definitionem kann es gar nicht richtig sein, denn ihr eigentliches Ergebnis (179,55%) ist kein möglicher Funktionswert des Wahrscheinlichkeitsmaßes. Hinzu kommt noch, dass sie die absolute Zahl 1,7955 (die auch noch ein wenig falsch errechnet ist) einfach mit einem %-Zeichen versieht, so dass es wieder plausibel aussieht. Ihr fällt nicht auf, dass dies keine Lösung der Aufgabe ist, kreuzt demnach auch einfach nichts an.
Folgendes sehe ich bei Ihr: Sie überprüft ihre Rechnung und die Ergebnisse nicht auf Plausibilität und baut ihr mathematisches Wissen nur auf dunkle Erinnerungen auf, die anscheinend aber nicht gut fundiert sind.
Mit diesem Beispiel hat man übrigens ein gutes Argument dafür, dass bedingte Wahrscheinlichkeit (die ja hier eine wesentliche Rolle spielt) begründet und bewiesen unterrichtet werden sollte, dass Schüler die Möglichkeit haben, die Zusammenhänge zu verstehen, anstatt dass man einfach die Pfadregeln auswendig lernen läßt.
| Studentin 8 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alter | Geschlecht | Studienrichtung Mathe | Mathe-LK | Vorgebildet | Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 |
| 19 | W | ja | nein | ja | falsch | falsch | falsch | richtig |
Interessant ist der Vergleich der Lösungsversuche 1 und 2 dieser Aufgabe. Hier stehen sich zwei Extreme gegenüber - der eine, der die richtige Lösung errechnet und die andere, die in der Notation ordentlicher ist und sich ein wenig mehr auskennt - der eine, der weiß, was er macht, und die andere, die weiß, wie sie es notiert. Im Unterricht hat man meistens beide Sorten von Schülern, die man dann irgendwie zusammenbringen muß, eine nicht triviale Aufgabe.
Aufgabe 3
Aufgabe 3 - Lösungsversuch 1 (Student 15)
Die Rechnungen und Notationen sehen sehr gebildet aus, der Student ist vorgebildet, das merkt man. Ich befürchte nur, dass er ein wenig zu gebildet ist, dass er die Einfachheit der Aufgabe nicht erkennt. Er mittelt die Daten erst, bevor er sie wieder miteinander verknüpft. Das Ergebnis ist dann leider falsch, aber - es sieht doch gut aus, was er da geschrieben hat, oder?
| Student 15 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alter | Geschlecht | Studienrichtung Mathe | Mathe-LK | Vorgebildet | Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 |
| 21 | M | nein | ja | ja | falsch | richtig | falsch | richtig |
Aufgabe 3 - Lösungsversuch 2 (Student 52)
Auch hier hat Student 52 die Aufgabe erkannt und gelöst - die Begründung ist so simpel wie die Aufgabe selber. Da braucht man nichts zu zu sagen ausser: Weiter so!
| Student 52 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alter | Geschlecht | Studienrichtung Mathe | Mathe-LK | Vorgebildet | Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 |
| 23 | M | ja | ja | ja | richtig | richtig | richtig | falsch |
Aufgabe 4
Aufgabe 4 - Lösungsversuch 1 (Student 12)
Dieser Lösungsversuch zeigt einen typischen Fehler: Man überlegt sich, wieviele Karten denn durch 4 und wieviele durch 6 teilbar sind, addiert sie und schon hat man, wieviele Karten durch 4 und 6 teilbar sind. Da müßten eigentlich die metakognitiven Alarmglocken schellen und ihn darauf hinweisen, dass dies nicht notwendigerweise so sein muß, es könnte ja sein, dass es Karten gibt, die sowohl durch 4 als auch durch 6 teilbar sind (wie in diesem Falle 12 und 24). Leider hat dieser Student das nicht bedacht und munter das Ergebnis angekreuzt.
| Student 12 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alter | Geschlecht | Studienrichtung Mathe | Mathe-LK | Vorgebildet | Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 |
| 20 | M | nein | ja | ja | falsch | richtig | richtig | falsch |
Aufgabe 4 - Lösungsversuch 2 (Student 52)
„Übermut tut selten gut“ - diesen Spruch möchte ich dem Studenten 52 zurufen. Nachdem er gut die ersten drei Aufgaben gelöst hat (siehe oben), geht er nun auch ganz forsch an die Aufgabe ran und übersieht, dass sowohl 10 als auch 20 nicht durch 4 oder 6 teilbar sind. Diesen groben Schnitzer kann ich mir nur als Flüchtigkeitsfehler erklären - die Gedanken im Kopf sind dabei richtig gewesen. Leider hat er aber durch seine Eile die Überprüfung sein gelassen.
| Student 52 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alter | Geschlecht | Studienrichtung Mathe | Mathe-LK | Vorgebildet | Aufgabe 1 | Aufgabe 2 | Aufgabe 3 | Aufgabe 4 |
| 23 | M | ja | ja | ja | richtig | richtig | richtig | falsch |
Interpretation der Ergebnisse
Als erstes bleibt festzuhalten, dass die Gestaltung des Tests gelungen war – es sind Lösungsversuche mit 100% Richtigkeit und welche mit 0% Richtigkeit vorhanden, die meisten Studenten haben um die 50% richtig gehabt. Alleine die erste Aufgabe scheint etwas zu schwer gewesen zu sein, dort sind die meisten richtigen Lösungen aufgrund von Zufall entstanden.
Festgestellt wurde: Allgemein sind die Studenten, die getestet wurden, besser als die 12-Klässler, die getestet wurden. Dies jedoch erfordert keine großartigen Erklärungsversuche – die Studenten sind schlichtweg mindestens 2 Jahre älter und zudem noch eine Auswahl, die sich eher für Mathematik interessiert.
Interessanter sind deshalb die Lösungsansätze und Begründungen, die die Studenten geliefert haben: Es scheint zwei Kategorien von Studenten zu geben: Die einen, die den Überblick haben, die Wahrscheinlichkeitsrechnung verstanden zu habe scheinen und für die sie kein Problem darstellen im Kopf, die dafür aber Defizite in einer strukturierten Darstellungsweise haben und zum anderen diejenigen, die zwar Ahnung von der Darstellung von Ergebnissen haben, die jedoch wenig Verständnis von dem haben, was sie machen. Eine weitere Beobachtung war zu machen: Gerade in der Vorlesung vor dem Test wurde der Binominalkoeffizient eingeführt (mit dem man bedingte Wahrscheinlichkeit nach dem Schema „ohne zurücklegen“ und „ohne Berücksichtigung der Reihenfolge“ berechnen kann). Dieser tauchte zusammenhangslos und ohne Begründung bei mehreren Aufgaben einfach so auf. Dies führt zu dem Schluss, dass diese nicht-verstehenden Studenten sehr Kalkül-orientiert gearbeitet haben, was im Sinne eines Verständnis-geleiteten Unterrichts, wie ich ihn oben angerissen habe, eher schädlich als nützlich ist. Sie scheinen einfach Formeln und Notationsformen im Hinterkopf zu haben und diese mit mehr oder weniger Überlegung anzuwenden. Hier müsste man sagen: Der Unterricht sollte sich hin zu einem Unterricht ändern, der mehr das Verständnis von Problemlöseverfahren fördert. Bei den anderen jedoch stellt man fest, dass sie nicht so recht wissen, wie genau sie etwas aufschreiben. Prinzipiell sind ja Ideen vorhanden, jedoch sind diese nicht bis ins letzte durchdacht und verinnerlicht. Deshalb denke ich, man sollte den Unterricht auch dahingehend verändern, dass Präzsion in der Darstellung verinnerlicht wird, wie es die Mathematik ja eigentlich auch fordert. Die Erfolge liegen dabei auf der Hand: Zum einen entstehen weniger Fehler durch falsche Interpretation des notierten und zum anderen kann man in einer präzisen Notation seine eigenen Gedanken bis ins letzte durchdenken und verarbeiten.
Zusammengefasst sind also die Ergebnisse: Eine stärkere Verständnis-Orientierung und eine größere Sorgfalt in Hinsicht auf Präzision der Darstellung könnten die Ergebnisse noch einmal immens verbessern, jedoch sind die jetzigen Ergebnisse durchaus im Durchschnitt.
Download
Hier gibt es eine komplette Liste aller Dateien, die im Zusammenhang mit dieser Ausarbeitung zur Verfügung stehen.
Copyright © Christian Datzko, 1996-2017. Alle Rechte vorbehalten. All rights reserved.